Entornos, puntos interiores, exteriores y de frontera, conjuntos abiertos y cerrados, puntos aislados y de accumulación: la explicación de los conceptos con muchos ejemplos y illustraciones
por Giulio Simeone
Roma, domingo 10 julio 2016
Los conceptos de entorno, punto interior, exterior y de frontera, conjunto abierto y cerrado, punto aislado y de accumulación son fundamentales en análisis y geometria: un etudiante que no haya bien entendido estos conceptos también a nivel intuitivo, es inútil que estudie todo el que sigue, incluidos los muy importantes conceptos de limite, derivada e integral. Entonces, además de dar al etudiante las definiciones, haremos lo mejor para hacerle asimilar los conceptos, de manera que ellos entren a hacer parte de su intuición y lo ayuden también a comprender los conceptos siguientes. Claramente, la rappresentación visual de los conceptos facilita mucho su asimilación: el espacio métrico más adecuado por esta finalidad es R², la mayoria de los ejemplos y de los illustraciones que presentaremos seran en el plano.
Entornos
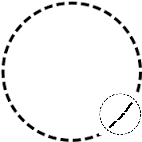
Dado un espacio métrico (S,d) y un su punto x, se llama entorno de x de rayo r el conjunto de todos los puntos y∈S que distan de x menos que r. En R² este conjunto corresponde al circulo de centro x y rayo r privado de los puntos de su circonferencia: de hecho, los puntos que distan exactamente r de x no hacen parte del conjunto. En la figura debajo, asì como en todas las siguientes, la circonferencia de trazo discontuo tiene el sentido que sus puntos no hacen parte del conjunto.
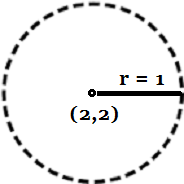
En R, el entorno de rayo r de un punto x corresponde al intervalo (x-r,x+r) privado de sus extremos.
Puntos interiores, exteriores y de frontera
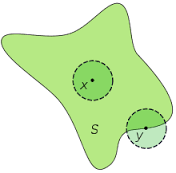
Un punto x se dice interior a un subconjunto A de un espacio métrico si existe un entorno de x totalmente contenido en A. En el caso del circulo, es facil ver que, en el caso de un punto interior al circulo, también muy cercano a la circonferencia, siempre existará un su entorno tan pequeño que no toca la circonferencia, mientras dado un punto que se encuentra a lo largo de la circonferencia, cada su entorno habrá puntos sea tanto dentro como fuera del circulo, como se puede ver en la figura debajo. Un punto de una circonferencia, entonces, no es interior a su circulo abierto, osea al conjunto de los puntos del circulo privado de su circonferencia: por eso existe todavia otra definición bien precisa que es la de punto de frontera del circulo.
En lo general, por cada subconjunto del plano cartesiano, sus puntos de frontera. como dice el nombre mismo, son todos los puntos que constituyen su delimitación. Formalmente, podemos decir que un punto x se llama de frontera por un conjunto A si cada su entorno contiene tanto puntos que pertenecen a A, como puntos que no pertenecen a A. Imaginamos de encontrarnos exactamente a lo largo de la frontera entre Chile y Argentina: cada “entorno” que contiene el punto donde nos encontramos, se encontrará en parte en Chile y en parte en Argentina.
La definición de punto exterior a un conjunto A es absolutamente analoga a la de punto interior.
Conjuntos abiertos y cerrados
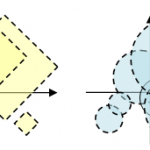
Suponemos ahora de tener dos subconjuntos constituidos del mismo cuadrado y que se diferencian solamente porque uno contiene el perimetro, y otro no lo contiene. Es evidente que la frontera de los dos conjuntos es exactamente la misma, la que es diferente es la classificación en conjuntos abiertos y cerrados. Un conjunto se llama abierto si todos sus puntos son puntos interiores; ya que, por lo antes dicho, un punto no puede ser al mismo tiempo interior y de frontera, este hecho implica que un conjunto abierto no contiene algun su punto de frontera. En referencia a nuestro ejemplo, un cuadrado que no contiene algun punto de su perimetro es un conjunto abierto. Viceversa, un conjunto se llama cerrado si contiene todos sus puntos de frontera: es el caso del cuadrato que contiene todos los puntos de su perimetro. Es importante notar que el mundo no se divide en conjuntos abiertos y cerrados: de hecho, un conjunto puede muy bien ser ni abierto ni cerrado, es el caso, por ejemplo, del cuadrado que contiene tres lados de su perimetro, pero no contiene el lado remanente. En la figura vemos los tres tipos de cuadrados descritos: un cuadrado abierto, un cuadrado cerrado, un cuadrado ni abierto ni cerrado.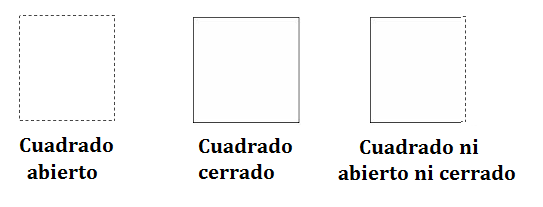
En R, un intervalo (a,b) privado de sus extremos es un conjunto abierto; un intervalo [a,b] que comprende sus extremos es un conjunto cerrado; un intervalo [a,b) o (a,b] que comprende solamente uno de sus dos extremos es un conjunto ni abierto, ni cerrado.
Punti di accumulazione
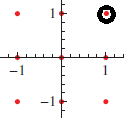
Pasamos ahora al concepto de punto de accumulaciòn. No todos los posibiles conjuntos del plano son visualmente representables con figuras geometricas: algunos pueden también contener unos o más puntos aislados. Por ejemplo, consideramos el conjunto Z² ⊂ R² de los puntos con coordenada entera, que es compuesto de infinitos puntos aislados: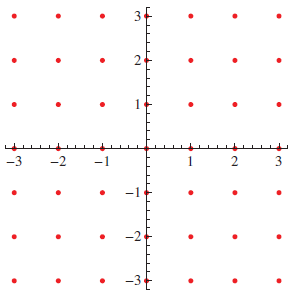
En R² el sentido de punto aislado es el que podemos esperar, la definición generalizada es la que sigue: un punto x de un subconjunto A de un espacio métrico (S,d) se llama aislado si existe un entorno que no contiene puntos de A diferentes de x mismo. En R² este hecho implica, como se puede ver de la figura, que el punto aislado está rodeado de puntos extraños a A.
Los puntos de A que no son aislados, osea los puntos que visualmente son en contacto con otros puntos de A, son puntos de accumulación por A. Un punto x se llama de accumulación por A si todos sus entornos contienen puntos de A diferentes de x mismo. Aunque los conceptos de punto aislado y de punto de accumulación por A sean alternativos, en el sentido que cada punto de A es aislado o de accumulación por A sin otras posibilidades, hay que aclarar algunas cosas:
- En R², si es verdadero que un punto aislado es totalmente rodeado de puntos extraños ad A, no necesariamente es verdad que un punto de accumulación es totalmente rodeado de puntos de A. Los puntos de una qualquier recta, por ejemplo, son de accumulación por la misma recta también no siendo completamente rodeados de puntos de la recta.
- Es muy importante notar que existen puntos que son de accumulación por un conjunto A también no pertenecendo al conjunto A mismo. Volviendo al ejemplo que hemos hecho antes del circulo abierto, osea privado de su circonferencia, ya deberia ser facil comprender que todos los puntos de la circonferencia son de accumulación por eso, porque qualquier su entorno contiene puntos de A.
Pero no existe solamente el ejemplo de una figura geometrica privada de su contorno, o, en R, de un intervalo abierto (a,b). En R^n todos los puntos que están “en contacto” con un determinado conjunto son de accumulación por eso; viceversa, pero, no todos los puntos de accumulación deben estar necesariamente “en contacto” con el conjunto. De hecho, por cuanto pueda parecer extraño, también un conjunto I formado solamente de puntos aislados puede tener un punto de accumulación, que obviamente no pertenece al conjunto I mismo, porque un punto que pertenece a I no puede ser de accumulación y aislado al mismo tiempo!! Consideramos, en R, el conjunto de todos los números de la forma 1/n con n∈N. Es claro que se trata de puntos todos aislados; pero vemos que, más n se vuelve grande, más la cuantidad 1/n se acerca a cero, sin obviamente nunca alcanzarlo: 1 sobre 1 miliardo es un número muy pequeño, pero siempre más grande de cero. Notamos ahora un fenómeno que por quien se acerca por la primera vez al analisis puede resultar sorprendente. Tomamos un qualquier entorno de cero, y suponemos que su rayo sea r. Suponemos r=1/a, y consideramos la parte entera |a|. De la figura debajo resulta evidente que el número 1/|a| no hace parte del entorno,y pero el número 1/(|a|+1) hace parte de eso!!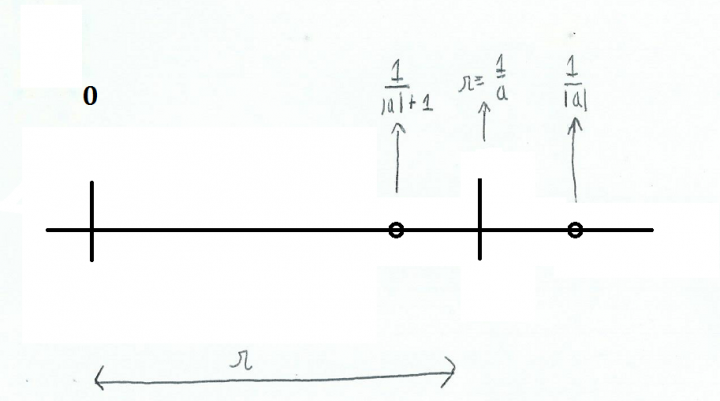
Este discurso, claramente, vale por qualquier entorno de 0, también extremamente pequeño. Cosa hemos visto? Que cada entorno de 0 contiene puntos que pertenecen al conjunto { 1/n, n∈N } claramente diferentes de 0, y que entonces 0 es un punto de accumulación por este conjunto!! En este caso, entonces, el punto de accumulación 0 no solo no pertenece al conjunto, pero no es ni siquiera en estrecho contacto con eso, porque, por cuanto pequeño sea un número de la forma 1/n, siempre existe un “gap” entre 0 y eso. Podemos más bien decir, en linea con la misma palabra, que los puntos del conjunto { 1/n, n∈N } “se acumulan” alrededor de lo cero.
