Intorni, punti interni, esterni e di frontiera, insiemi aperti e chiusi, punti isolati e di accumulazione: i concetti spiegati con molti esempi ed illustrazioni
di Giulio Simeone
Roma, venerdì 1 luglio 2016
I concetti di intorno, di punto interno, esterno e di frontiera, di insieme aperto, di insieme chiuso, di punto di accumulazione, sono fondamentali in analisi ed in geometria: uno studente che non abbia ben chiari questi concetti anche a livello intuitivo, è inutile che studi tutto quello che segue, compresi gli importantissimi concetti di limite, di derivata e di integrale. Noi quindi, oltre a dare allo studente le definizioni, faremo del nostro meglio per fargli assimilare i concetti, in modo che essi entrino a far parte della sua intuizione e gli rendano più semplice anche la comprensione delle nozioni successive. Chiaramente, la rappresentazione visiva dei concetti facilita parecchio la loro assimilazione: lo spazio metrico più adatto a tale scopo è R², la maggior parte degli esempi e delle illustrazioni che presenteremo saranno quindi sul piano.
Intorni
Dato uno spazio metrico (S,d) e un suo punto x, si definisce intorno di x di raggio r l’insieme di tutti i punti y∈S che distano da x meno di r. In R² tale insieme corrisponde al cerchio di centro x e raggio r privato dei punti della sua circonferenza: infatti, i punti che distano esattamente r da x non fanno parte dell’insieme. Nella figura qui sotto, così come in tutte quelle che seguiranno, la circonferenza tratteggiata sta a significare che i suoi punti non fanno parte dell’insieme.
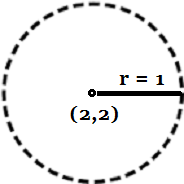
In R, l’intorno di raggio r di un punto x corrisponde all’intervallo (x-r,x+r) privato dei suoi estremi.
Punti interni, esterni e di frontiera
Un punto x si dice interno ad un sottoinsieme A di uno spazio metrico se esiste un intorno di x totalmente contenuto in A. Nel caso del cerchio, è facile vedere che, nel caso di un punto interno al cerchio, anche molto vicino alla circonferenza, esisterà sempre un suo intorno talmente piccolo che non tocca la circonferenza, mentre dato un punto che si trova sulla circonferenza, ogni suo intorno avrà punti sia dentro che fuori il cerchio, come si vede dal disegno qui sotto. Un punto di una circonferenza, quindi, non è interno al suo cerchio aperto, ovvero all’insieme dei punti del cerchio privato della circonferenza: per esso, però, c’è un’altra definizione ben precisa che è quella di punto di frontiera del cerchio.
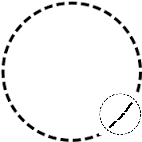In generale, per ogni sottoinsieme del piano cartesiano, i suoi punti di frontiera. come dice il nome stesso, sono tutti i punti che costituiscono la sua delimitazione. Formalmente, possiamo dire che un punto x si dice di frontiera per un insieme A se ogni suo intorno contiene sia punti che appartengono ad A, che punti che non vi appartengono. Immaginiamo di trovarci esattamente lungo il confine tra Italia ed Austria: ogni “intorno” che contiene il punto dove noi ci troviamo, si troverà in parte in Italia e in parte in Austria.
La definizione di punto esterno ad un insieme A è assolutamente analoga a quella di punto interno.
Insiemi aperti e chiusi
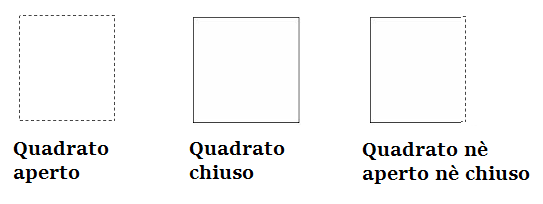
Supponiamo adesso di avere due sottoinsiemi costituiti dallo stesso quadrato e che si differenziano soltanto perchè uno contiene il perimetro, ed uno non lo contiene. E’ del tutto evidente che la frontiera dei due insiemi è esattamente la stessa, quella che cambia è la classificazione in insiemi aperti e chiusi. Un insieme si dice aperto se tutti i suoi punti sono punti interni; visto che, per quanto abbiamo detto prima, un punto non può essere allo stesso tempo interno oppure di frontiera, ciò implica che un insieme aperto non contiene nessun punto di frontiera. In riferimento al nostro esempio, un quadrato che non contiene nessun punto del suo perimetro è un insieme aperto. Viceversa, un insieme si definisce chiuso se contiene tutti i suoi punti di frontiera: è il caso del quadrato che contiene tutti i punti del suo perimetro. E’ importante notare che il mondo non si divide in insiemi aperti e chiusi: infatti un insieme può benissimo non essere nè aperto nè chiuso, è il caso, ad esempio, del quadrato che contiene tre dei lati del suo perimetro, ma non contiene il lato rimanente.Nella figura vediamo i tre tipi di quadrato descritti: un quadrato aperto, un quadrato chiuso, un quadrato nè aperto nè chiuso.
In R, un intervallo (a,b) privo dei suoi estremi è un insieme aperto; un intervallo [a,b] che comprende i suoi estremi è un insieme chiuso; un intervallo [a,b) oppure (a,b] che comprende uno solo dei suoi due estremi è un insieme nè aperto, nè chiuso.
Punti di accumulazione
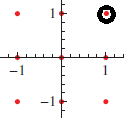
Passiamo adesso al concetto di punto di accumulazione. Non tutti i possibili insiemi del piano sono visivamente rappresentabili con figure geometriche: alcuni possono contenere anche uno o più punti isolati. Per esempio, prendiamo l’insieme Z² ⊂ R² dei punti a coordinata intera, che è formato da infiniti punti isolati: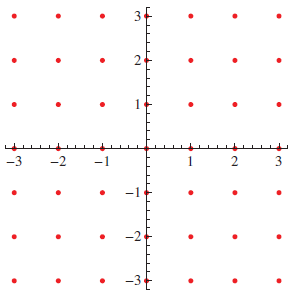
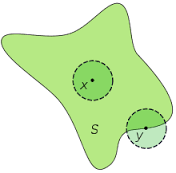
In R² il significato di punto isolato è quello che ci si aspetta, la definizione generalizzata è la seguente: un punto x di un sottoinsieme A di uno spazio metrico (S,d) si dice isolato se esiste un intorno che non contiene punti di A diversi da x stesso. In R² ciò implica, come si vede dalla figura, che il punto isolato è circondato da punti estranei ad A.
I punti di A che non sono isolati, ovvero i punti che visivamente sono a contatto con altri punti di A, sono punti di accumulazione per A. Un punto x si dice di accumulazione per A se tutti i suoi intorni contengono punti di A diversi da x stesso. Per quanto i concetti di punto isolato e di punto di accumulazione siano alternativi, nel senso che ogni punto di A è isolato oppure di accumulazione per A senza altre possibilità, vanno chiarite alcune cose:
-
- In R², se è vero che un punto isolato è totalmente circondato da punti estranei ad A, non necessariamente un punto di accumulazione è totalmente circondato da punti di A. I punti di una qualsiasi retta, ad esempio, sono di accumulazione per la stessa retta pur non essendo completamente circondati da punti della retta.
- E’ importantissimo notare che esistono punti che sono di accumulazione per un insieme A pur non appartenendo all’insieme A stesso. Tornando all’esempio che abbiamo fatto prima del cerchio aperto, ovvero privo della circonferenza, ormai ci dovrebbe risultare abbastanza facile capire che tutti i punti della circonferenza sono d’accumulazione per esso, perchè qualsiasi loro intorno contiene punti di A.
Però non esiste soltanto l’esempio di una figura geometrica priva del suo contorno, oppure, in R, di un intervallo aperto (a,b). In R^n tutti i punti che sono “a contatto” con un determinato insieme sono d’accumulazione per esso; viceversa, però, non tutti i punti d’accumulazione devono essere necessariamente “a contatto” con l’insieme. Infatti, per quanto possa sembrare strano, anche un insieme I formato soltanto da punti isolati può avere un punto di accumulazione, che naturalmente non appartiene all’insieme I stesso, perchè un punto appartenente a I non può essere d’accumulazione e isolato allo stesso tempo!! Prendiamo infatti, in R, l’insieme di tutti i numeri della forma 1/n con n∈N. E’ chiaro che si tratta di punti tutti isolati; però vediamo che, più n diventa grande, più la quantità 1/n si avvicina allo zero, senza ovviamente raggiungerlo mai: 1 su 1 miliardo è un numero piccolissimo, ma sempre maggiore di zero. Notiamo adesso un fenomeno che per chi si avvicina per la prima volta all’analisi può risultare sorprendente. Prendiamo un intorno qualsiasi di zero, e supponiamo che il suo raggio sia r. Supponiamo r=1/a, e consideriamo la parte intera |a|. Dalla figura risulta evidente che il numero 1/|a| non fa parte dell’intorno, e però il numero 1/(|a|+1) vi fa parte!!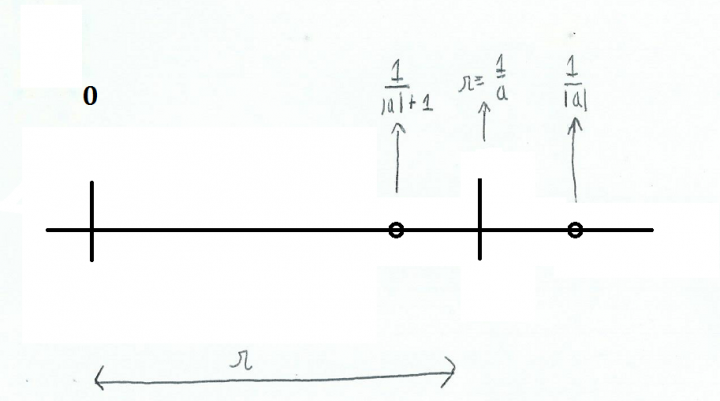
.Questo discorso, chiaramente, vale per qualunque intorno di 0, anche estremamente piccolo. Cosa abbiamo visto? Che ciascun intorno di 0 contiene punti appartenenti all’insieme { 1/n, n∈N } chiaramente diversi da 0, e che quindi 0 è un punto di accumulazione per tale insieme!! In questo caso, quindi il punto di accumulazione 0 non solo non appartiene all’insieme, ma non è neanche a stretto contatto con esso, perchè, per quanto piccolo sia un numero della forma 1/n, esiste sempre un “gap” tra 0 ed esso. Possiamo piuttosto dire, in linea con la parola stessa, che i punti dell’insieme { 1/n, n∈N } “si accumulano” intorno allo zero.
